As described in chapter 3 on "IR Thermometers & Pyrometers", thermocouples have been used as detectors in radiation thermometry for many decades. Often, a series of thermocouples, or thermopile, was the thermal detector of choice. But in more recent years a new class of low-cost, self-powered "infrared thermocouples" has been developed, and has opened up a broad market for non-contact temperature measurement in such industries as food, electronics, paper, pharmaceutical, plastics, rubber, and textiles.
All infrared thermocouple sensors work in a fashion similar to a standard thermocouple: a small millivoltage or electromotive force (emf) relates to the temperature being measured. To correctly apply any such instrument, the user or designer must be aware of certain basic characteristics of all thermocouples and the circuitry involved. Just how does the thermocouple function in providing a usable emf measuring signal? And what is important to observe so far as metering that signal to accurately indicate the measured temperature? What is the effect of changes in ambient temperature--at the thermocouple and at the meter? A discussion with reference to Figure 4-1 will help make such points clear.
Thermocouple Basics
Let's start with T. J. Seebeck, who in 1821 discovered what is now termed the thermoelectric effect. He noted that when two lengths of dissimilar metal wires (such as iron and Constantan) are connected at both ends to form a complete electric circuit, an emf is developed when one junction of the two wires is at a different temperature than the other junction.
Basically, the developed emf (actually a small millivoltage) is dependent upon two conditions: (1) the difference in temperature between the hot junction and the cold junction. Note that any change in either junction temperature can affect the emf value and (2) the metallurgical composition of the two wires.
Although a "thermocouple" is often pictured as two wires joined at one end, with the other ends not connected, it is important to remember that it is not a true thermocouple unless the other end is also connected! It is well for the user to remember this axiom: "Where there is a hot junction there is always a cold or reference junction" (even though it may seem hidden inside an instrument 1,000 feet away from the hot junction).
Still in Seebeck's century, two other scientists delved deeper into how the emf is developed in a thermoelectric circuit. Attached to their names are two phenomena they observed--
the Peltier effect (for Jean Peltier in 1834) and the Thompson effect
(for Sir William Thompson a.k.a Lord Kelvin in 1851). Without getting into the theories involved, we can state that the Peltier effect is the emf resulting solely from the contact of the two dissimilar wires. Its magnitude varies with the temperature at the juncture. Similarly, the Thompson effect can be summarized as having to do with emf's produced by a temperature gradient along a metal conductor. Since there are two points of contact and two different metals or alloys in any thermocouple, there are two Peltier and two Thompson emfs. The net emf acting in the circuit is the result of all the above named effects.
Polarity of the net emf is determined by (a) the particular metal or alloy pair that is used (such as iron-constantan) and (b) the relationship of the temperatures at the two junctions. The value of the emf can be measured by a potentiometer, connected into the circuit at any point.
In summary, the net emf is a function primarily of the temperature difference between the two junctions and the kinds of materials used. If the temperature of the cold junction is maintained constant, or variations in that temperature are compensated for, then the net emf is a function of the hot junction temperature.
In most installations, it is not practical to maintain the cold junction at a constant temperature. The usual standard temperature for the junction (referred to as the "reference junction") is 32°F (0°C). This is the basis for published tables of emf versus temperature for the various types of thermocouples.
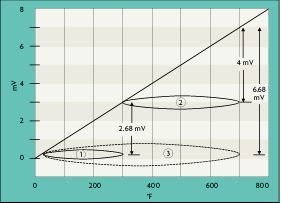
The Law of Intermediate Temperatures provides a means of relating the emf generated under ordinary conditions to what it should be for the standardized constant temperature (e.g., 32°F). Referring to Figure 4-1, which shows thermocouples 1 and 2 made of the same two dissimilar metals; this diagram will provide an example of how the law works. Thermocouple 1 has its cold junction at the standard reference temperature of 32°F and its hot junction at some arbitrary intermediate reference temperature (in this case, 300°F). It generates 2.68 mv. Thermocouple 2 has its cold junction at the intermediate reference point of 300°F and its hot junction at the temperature being measured (700°F). It generates 4.00 mv. The Law of Intermediate Temperatures states the sum of the emfs generated by thermocouples 1 and 2 will equal the emf that would be generated by a single thermocouple (3, shown dotted) with its cold junction at 32°F and its hot junction at 700°F, the measured temperature. That is, it would hypothetically read 6.68 mv and represent the "true" emf according to the thermocouple's emf vs. temperature calibration curve.
Based upon this law, the manufacturer of an infrared thermocouple need only provide some means of substituting for the function of thermocouple 1 to provide readings referenced to the standard 32°F cold junction. Many instruments accomplish this with a temperature-sensitive resistor which measures the variations in temperature at the cold junction (usually caused by ambient conditions) and automatically develops the proper voltage correction.
Another use of this law shows that extension wires having the same thermoelectric characteristics as those of the thermocouple can be introduced into the thermocouple circuit without affecting the net emf of the thermocouple.
In practice, additional metals are usually introduced into the thermocouple circuit. The measuring instrument, for example, may have junctures that are soldered or welded. Such metals as copper, manganin, lead, tin, and nickel may be introduced.
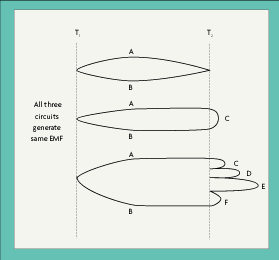
Would not additional metals like this modify the thermocouple's emf? Not so, according to the Law of Intermediate Metals. It states that the introduction of additional metals will have no effect upon the emf generated so long as the junctions of these metals with the two thermocouple wires are at the same temperature. This effect is illustrated in Figure 4-2, with A and B representing the thermocouple wires.
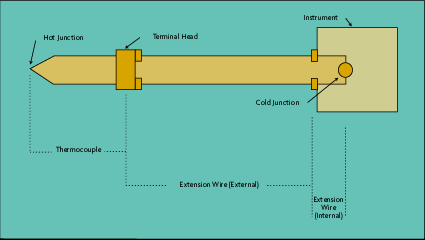
A practical example of this law is found in the basic thermoelectric system shown in Figure 4-3. The instrument can be located at some distance from the point of measurement where the thermocouple is located. Several very basic and practical points are illustrated in this elementary circuit diagram:
Quite often the most convenient place to provide the cold junction compensation is in the instrument, remote from the process.
With the compensation means located in the instrument, in effect, the thermoelectric circuit is extended from the thermocouple hot junction to the reference (cold) junction in the instrument.
The actual thermocouple wires normally terminate relatively near the hot junction. Conventional couples have what is called a "terminal head" at which point interconnecting wires, known as "extension wires" are required as shown. Since these wires are in the thermoelectric circuit, they must essentially match the emf vs. temperature characteristics of the thermocouple.
With the cold junction located inside the instrument, internal extension wires of the proper materials must be used between the instrument terminals and the cold junction.
With this set-up, there are in effect three added thermocouples in the circuit: one in the thermocouple assembly, one in the external extension wire, and in the internal extension wire. However, according to the Law of Intermediate Temperatures, the actual temperatures at the terminal head and at the instrument terminals is of no consequence: the net effect of the three thermocouples is as if one thermocouple ran from the hot junction to the cold junction.
The Infrared Thermocouple
Over the past decade or two, there has been a mushroom growth in the small, application-specific designs of infrared thermocouples. These contain a sophisticated optical system and electronic circuitry that belie the simplicity of their external, tube-like appearance. They use a special proprietary design of thermopile which develops enough emf to be connected directly to a conventional thermocouple type potentiometer or transmitter for all types of indication, recording, and control.
A wide variety of these devices are commercially available, covering temperature ranges from -50 to 5000°F
(-45 to 2760°C) with up to 0.01°C precision. The range of models includes:
Standard units, simulating the thermocouple outputs J, K, T, E, R, and S and offering 12 different fields of view from 1:2 to 100:1. Minimum spot size is 1 mm and focused spot sizes available range from 4 mm to 12 mm.
Handheld scanning models for such applications as accurate scanning of electrical equipment and NIST traceable surface temperature calibration--a must for ISO 9001, 9002, 9003 programs.
Thermal switches that act like photocells for use in production line quality inspection of thermal processes with line speeds of up to 1000 feet per minute.
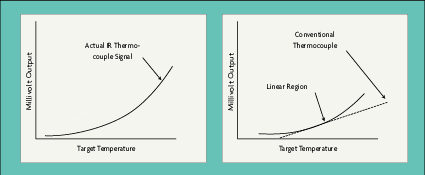
All infrared thermocouples are self-powered, using only the incoming infrared radiation to produce an mv output signal through thermoelectric effects. The signal thus follows the rules of radiation thermal physics and produces a curve as shown in Figure 4-4.
Over a specific, relatively narrow temperature range, the output is sufficiently linear to produce an mv output that can be closely matched to the mv vs. temperature curve of a given thermocouple type (Figure 4-4). What's more, the designer can match the two curves to be within a degree of tolerance such as ±2%, as specified by the buyer.
Each model is specifically designed for optimum performance in the region of best linear fit with the thermocouple's mv vs. temperature curve. The sensor can be used outside that range, however, by simply calibrating the readout device appropriately. Once so calibrated, the output signal is smooth and continuous over the entire range of the thermocouple, and will maintain a 1% repeatability over the entire range.
The user can select a model to provide, say, a 2% accuracy, by referring in the supplier's literature to a Range Chart which provides a vertical list of "Range Codes" with a corresponding Temperature Range over which 2% accuracy is to be expected. The user also specifies the type of thermocouple (J, K, etc).
A typical infrared thermocouple comprises a solid, hermetically-sealed, fully-potted system. As such, even during severe service, it does not change either mechanically or metallurgically. It contains no active electronic components and no power source other than the thermocouple itself. Thus, suppliers rate its long-term repeatability, conservatively, at 1%.
Long term accuracy is influenced by the same factors that affect reliability. In comparison to the application of conventional thermocouples, the infrared thermocouple is well protected inside a rigid, stainless steel housing. Along with the solid, fully-potted construction, this design essentially eliminates the classical drift problems of conventional thermocouples. Double annealing at temperatures above 212°F (100°C) helps ensure long term stability.
Installation Guidelines
Like all radiation-based sensing systems, the infrared thermocouple must be calibrated for specific surface properties of the object being measured, including amount of heat radiated from the target surface and environmental heat reflections.
The calibration is performed by measuring the target surface temperature with a reliable independent surface-temperature probe. One such device is a handheld infrared thermometer with a built-in automatic emissivity compensation system.
The following procedure is recommended:
(1) Install the infrared thermocouple as close as practical to view the target to be measured.
(2) Connect the infrared thermocouple to the supervisory controller or data acquisition system in standard fashion (including shield). As with conventional thermocouples, the red wire is always negative.
(3) Bring the process up to normal operating temperature and use the hand-held radiation thermometer to measure the actual target temperature.
(4) Make the proper adjustments on the readout instrument so that its calibration matches the reading of the handheld device.
 CLOSE
CLOSE




