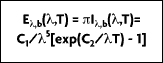All matter--animate or inanimate, liquid, solid, or gas--constantly exchanges thermal energy in the form of electromagnetic radiation with its surroundings. If there is a temperature difference between the object in question and its surroundings, there will be a net energy transfer in the form of heat; a colder object will be warmed at the expense of its surroundings, a warmer object cooled. And if the object in question is at the same temperature as its surrounding, the net radiation energy exchange will be zero.
In either case, the characteristic spectrum of the radiation depends on the object and its surroundings' absolute temperatures. The topic of this volume, radiation thermometry, or more generally, non-contact temperature measurement, involves taking advantage of this radiation dependence on temperature to measure the temperature of objects and masses without the need for direct contact.
Radiation Basics
The development of the mathematical relationships to describe radiation were a major step in the development of modern radiation thermometry theory. The ability to quantify radiant energy comes, appropriately enough, from Planck's quantum theory. Planck assumed that radiation was formed in discrete energy packages called photons, or quanta, the magnitude of which are dependent on the wavelength of the radiation. The total energy of a quantum, E, is found by multiplying Planck's constant, h = 6.6256 x 10
-34, and, the radiation frequency,
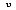
, in cycles per second.
In 1905, Albert Einstein postulated that these quanta are particles moving at the speed of light, c = 2.9979 x 10
8 m/s. If these photons traveled at the speed of light, then they must obey the theory of relativity, stating E
2 = c
2p
2 , and each photon must have the momentum
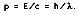
The frequency can be found by dividing the speed of light by its particle wavelength
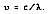
Substituting for momentum:
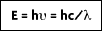
From this equation, it is apparent that the amount of energy emitted depends on the wavelength (or frequency). The shorter the wavelength, the higher the energy.
Emitted radiation consists of a continuous, non-uniform distribution of monochromatic (single-wavelength) components, varying widely with wavelength and direction. The amount of radiation per unit wavelength interval, referred to as the spectral concentration, also varies with wavelength. And the magnitude of radiation at any wavelength as well as the spectral distribution vary with the properties and temperature of the emitting surface. Radiation is also directional. A surface may prefer a particular direction to radiate energy. Both spectral and directional distribution must be considered in studying radiation.
Wavelength can be thought of as a type of address to find where a ray's energy is located. The map containing all the wavelengths of electromagnetic radiation is called the electromagnetic spectrum (see the inside front cover of this volume). The short wavelengths are the gamma rays, x-rays, and ultraviolet (UV) radiation, containing the highest amount of energy emitted. The intermediate portion of the spectrum, the heat region, extends from approximately 0.1 to 1000

(micrometers or microns: 1,000,000 microns = 1 meter), and includes a portion of the ultraviolet and all of the visible (VIS) and infrared (IR) waves. This portion is termed thermal radiation, and is important in the study of heat transfer and radiation thermometry.
Non-contact temperature sensors work in the infrared portion of the spectrum. The infrared range falls between 0.78 microns and 1000 microns in wavelength, and is invisible to the naked eye. The infrared is region can be divided into three regions: near-infrared (0.78-3.0 microns); middle infrared (3-30 microns); and far infrared (30-300 microns). The range between 0.7 microns and 14 microns is normally used in infrared temperature measurement. The divisions have been related to the transmission of the atmosphere for different types of applications.
Blackbody Concepts
Incident energy striking an object from the surroundings, can be absorbed by the object, reflected by the object, or transmitted through the object (if it is not opaque) as seen in Figure 2-1. If the object is at a constant temperature, then the rate at which it emits energy must equal the rate at which it absorbs energy, otherwise the object would cool (emittance greater than absorption), or warm (emittance less than absorption). Therefore, for bodies at constant temperature, the emittance (absorption), the reflection and the transmittance of energy equals unity.
Central to radiation thermometry is the concept of the blackbody.
In 1860, Kirchhoff defined a blackbody as a surface that neither reflects or transmits, but absorbs all incident radiation, independent of direction and wavelength. The fraction of radiation absorbed by a real body is called absorptivity,
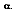
For an ideal blackbody, the absorptivity is 1.0
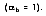
. For non-blackbodies, the absorption is a fraction of the radiation heat transfer incident on a surface, or
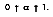
Hence, in term of radiation heat transfer, q":
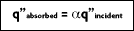
In addition to absorbing all incident radiation,
a blackbody is a perfect radiating body. To describe the emitting capabilities of a surface in comparison to a blackbody, Kirchoff defined emissivity
of a real surface as the ratio of the thermal radiation emitted by a surface at a given temperature to that of a blackbody at the same temperature and for the same spectral and directional conditions.
This value also must be considered by a non-contact temperature sensor when taking a temperature measurement.
The total emissivity for a real surface is the ratio of the total amount of radiation emitted by a surface in comparison to a blackbody at the same temperature. The tables beginning on p. 72 give representative emissivity values for a wide range of materials. If precise temperature measurements are required, however,
the surface's actual emittivity value should be obtained. (Although often used interchangeably, the terms emissivity and emittivity have technically different meanings. Emissivity refers to a property of a material, such as cast iron, whereas emittivity refers to a property of a specific surface.)
In 1879, Stefan concluded based on experimental results that the radiation emitted from the surface of an object was proportional to the fourth power of the absolute temperature of the surface. The underlying theory was later developed by Boltzmann, who showed that the radiation given off by a blackbody at absolute temperature T
s (K) is equal to:
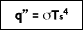
where
( is the Stefan-Boltzmann constant
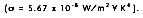
The heat transfer rate by radiation for a non-blackbody, per unit area is defined as:
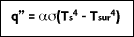
where T
s is the surface temperature and T
sur is the temperature of the surroundings.
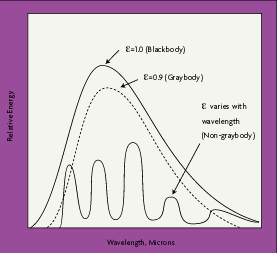
Although some surfaces come close to blackbody performance, all real objects and surfaces have emissivities less than 1. Non-blackbody objects are either graybodies, whose emissivity does vary with wavelength, or non-graybodies, whose emissivities vary with wavelength. Most organic objects are graybodies, with an emissivity between 0.90 and 0.95 (Figure 2-2).
The blackbody concept is important because it shows that radiant power depends on temperature. When using non-contact temperature sensors to measure the energy emitted from an object, depending on the nature of the surface, the emissivity must be taken into account and corrected. For example, an object with an emissivity of 0.6 is only radiating 60% of the energy of a blackbody. If it is not corrected for, the temperature will be lower than the actual temperature. For objects with an emissivity less than 0.9, the heat transfer rate of a real surface is identified as:
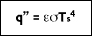
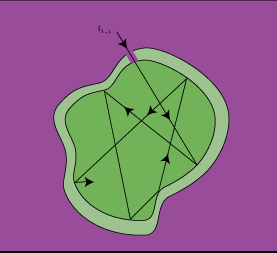
The closest approximation to a blackbody is a cavity with an interior surface at a uniform temperature T
s, which communicates with the surroundings by a small hole having a diameter small in comparison to the dimensions of the cavity (Figure 2-3). Most of the radiation entering the opening is either absorbed or reflected within the cavity (to ultimately be absorbed), while negligible radiation exits the aperture. The body approximates a perfect absorber, independent of the cavity's surface properties.
The radiation trapped within the interior of the cavity is absorbed and reflected so that the radiation within the cavity is equally distributed--some radiation is absorbed and some reflected. The incident radiant energy falling per unit time on any surface per unit area within the cavity is defined as the irradiance
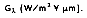
If the total irradiation G (W/m
2) represents the rate at which radiation is incident per unit area from all directions and at all wavelengths, it follows that:
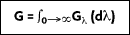
If another blackbody is brought into the cavity with an identical temperature as the interior walls of the cavity, the blackbody will maintain its current temperature. Therefore, the rate at which the energy absorbed by the inner surface of the cavity will equal the rate at which it is emitted.
In many industrial applications, transmission of radiation, such as through a layer of water or a glass plate, must be considered. For a spectral component of the irradiation, portions may be reflected, absorbed, and transmitted. It follows that:
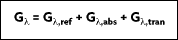
In many engineering applications, however, the medium is opaque to the incident radiation. Therefore,
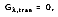
and the remaining absorption and reflection can be treated as surface phenomenon. In other words, they are controlled by processes occurring within a fraction of a micrometer from the irradiated surface. It is therefore appropriate to say that the irradiation is absorbed and reflected by the surface, with the relative magnitudes of
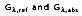
depending on the wavelength and the nature of the surface.
Radiation transfer by a non-blackbody encompasses a wide range of wavelengths and directions. The spectral hemispherical emissive power,
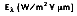
is defined as the rate at which radiation is emitted per unit area at all possible wavelengths and in all possible directions from a surface, per unit wavelength
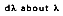
and per unit surface area.
Although the directional distribution of surface emission varies depends on the surface itself, many surfaces approximate diffuse emitters. That is, the intensity of emitted radiation is independent of the direction in which the energy is incident or emitted. In this case, the total, hemispherical (spectral) emissive power,
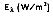
is defined as:
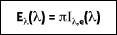
or
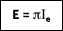
where I
e is the total intensity of the emitted radiation, or the rate at which radiant energy is emitted at a specific wavelength, per unit area of the emitting surface normal to the direction, per unit solid angle about this direction, and per unit wavelength. Notice that
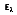
is a flux based on the actual surface area, where
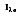
is based on the projected area. In approximating a blackbody, the radiation is almost entirely absorbed by the cavity. Any radiation that exits the cavity is due to the surface temperature only.
The spectral characteristics of blackbody radiation as a function of temperature and wavelength were determined by Wilhelm Wien in 1896. Wien derived his law for the distribution of energy in the emission spectrum as:
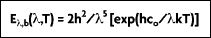
where
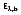
(b for blackbody) represents the intensity of radiation emitted by a blackbody at temperature T, and wavelength
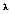
per unit wavelength interval, per unit time, per unit solid angle, per unit area. Also, h = 6.626 x 10
-24 J•s and k = 1.3807 x 10
-23 J•K
-1 are the universal Planck and Boltzman constants, respectively; c
o = 2.9979 x 10
8 m/s is the speed of light in a vacuum, and T is the absolute temperature of the blackbody in Kelvins (K).
Due to the fact that deviations appeared between experimental results and the equation, Planck suggested in 1900 a refinement that better fit reality:
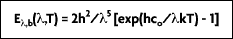
It is from this equation that Planck postulated his quantum theory. A more convenient expression for this equation, referred to as the Planck distribution law (Figure 2-4), is:
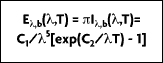
where the first and second radiation constants are
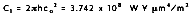
and
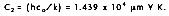
Planck's distribution shows that as wavelength varies, emitted radiation varies continuously. As temperature increases, the total amount of energy emitted increases and the peak of the curve shifts to the left, or toward the shorter wavelengths. In considering the electromagnetic spectrum, it is apparent that bodies with very high temperatures emit energy in the visible spectrum as wavelength decreases. Figure 2-4 also shows that there is more energy difference per degree at shorter wavelengths.
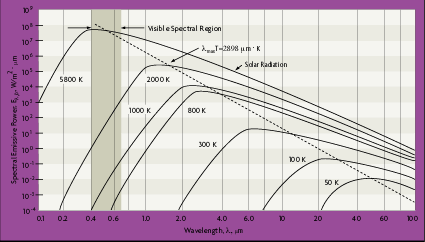
From Figure 2-4, the blackbody spectral distribution has a maximum wavelength value, lmax, which depends on the temperature. By differentiating equation 2.12 with respect to
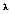
and setting the result equal to zero:
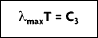
where the third radiation constant, C3 = 2897.7
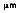
• K.
This is known as Wien's displacement law. The dashed line in Figure 2-4 defines this equation and locates the maximum radiation values for each temperature, at a specific wavelength. Notice that maximum radiance is associated with higher temperatures and lower wavelengths.
From Blackbodies to Real Surfaces
At first it would seem that a radiation thermometer would utilize the entire spectrum, capturing most of the radiant emission of a target in its particular temperature range. There are several reasons why this is not practical.
In the equations for infrared radiation derived above, it was found that at very low wavelengths, the radiance increases rapidly with temperature, in comparison to the increase at higher wavelengths, as shown in Figure 2-4. Therefore, the rate of radiance change is always greater at shorter wavelengths. This could mean more precise temperature measurement and tighter temperature control. However, at a given short wavelength there is a lower limit to the temperature that can be measured. As the process temperature decreases, the spectral range for an infrared thermometer shifts to longer wavelengths and becomes less accurate.
The properties of the material at various temperatures must also be considered. Because no material emits as efficiently as a blackbody at a given temperature, when measuring the temperature of a real target, other considerations must be made. Changes in process material emissivity, radiation from other sources, and losses in radiation due to dirt, dust, smoke, or atmospheric absorption can introduce errors.
The absorptivity of a material is the fraction of the irradiation absorbed by a surface. Like emission, it can be characterized by both a directional and spectral distribution. It is implicit that surfaces may exhibit selective absorption with respect to wavelength and direction of the incident radiation. However, for most engineering applications, it is desirable to work with surface properties that represent directional averages. The spectral, hemispherical absorptivity for a real surface
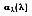
is defined as:
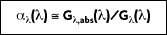
where
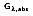
is the portion of irradiation absorbed by the surface. Hence,
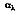
depends on the directional distribution of the incident radiation, as well as on the wavelength of the radiation and the nature of the absorbing surface. The total, hemispherical absorptivity,
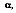
represents an integrated average over both directional and wavelength. It is defined as the fraction of the total irradiation absorbed by a surface, or:
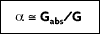
The value of
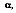
depends on the spectral distribution of the incident radiation, as well as on its directional distribution and the nature of the absorbing surface. Although
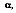
is independent on the temperature of the surface, the same may not be said for the total, hemispherical emissivity. Emissivity is strongly temperature dependent.
The reflectivity of a surface defines the fraction of incident radiation reflected by a surface. Its specific definition may take several different forms. We will assume a reflectivity that represents an integrated average over the hemisphere associated with the reflected radiation to avoid the problems from the directional distribution of this radiation.
The spectral, hemispherical reflectivity
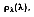
then, is defined as the spectral irradiation that is reflected by the surface. Therefore:
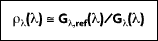
where

is the portion of irradiation reflected by the surface. The total, hemispherical reflectivity r is then defined as:
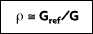
If the intensity of the reflected radiation is independent of the direction of the incident radiation and the direction of the reflected radiation, the surface is said to be diffuse emitter.
In contrast, if the incident angle is equivalent to the reflected angle, the surface is a specular reflector. Although no surface is perfectly diffuse or specular, specular behavior can be approximated by polished or mirror-like surfaces. Diffuse behavior is closely approximated by rough surfaces and is likely to be encountered in industrial applications.
Transmissivity is the amount of radiation transmitted through a surface. Again, assume a transmissivity that represents an integrated average. Although difficult to obtain a result for transparent media, hemispherical transmissivity is defined as:
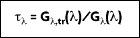
where
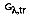
is the portion of irradiation reflected by the surface. The total hemispherical transmissivity is:
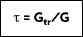
The sum of the total fractions of energy absorbed
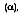
reflected
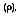
and transmitted
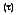
must equal the total amount of radiation incident on the surface. Therefore, for any wavelength:
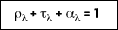
This equation applies to a semitransparent medium. For properties that are averaged over the entire spectrum, it follows that:
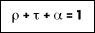
For a medium that is opaque, the value of transmission is equal to zero. Absorption and reflection are surface properties for which:
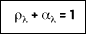
and
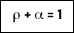
For a blackbody, the transmitted and reflected fractions are zero and the emissivity is unity.
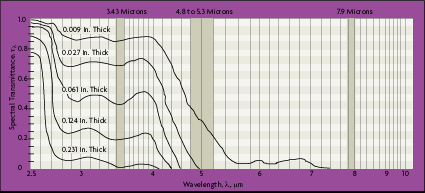
An example of a material whose emissivity characteristics change radically with wavelength is glass. Soda-lime glass is an example of a material which drastically changes its emissivity characteristics with wavelength (Figure 2-5). At wavelengths below about 2.6 microns, the glass is highly transparent and the emissivity is nearly zero. Beyond 2.6 microns, the glass becomes increasingly more opaque. Beyond 4 microns, the glass is completely opaque and the emissivity is above 0.97.
 CLOSE
CLOSE