The International Temperature Scale of 1990 (ITS-90)

H. Preston-Thomas
President of the Comité Consultatif de Thermométrie and Vice-President of the Comité International des Poids et Mesures Division of Physics, National Research Council of Canada, Ottawa, K1A OS1 Canada

Received: October 24, 1989

Introductory Note

The official French text of the ITS-90 is published by the BIPM as part of the Prochès-verbaux of the Comité International des Poids et Mesures (CIPM). However, the English version of the text reproduced here has been authorized by the Comité Consultatif de Thermométrie (CCT) and approved by the CIPM.

The International Temperature Scale of 1990

The International Temperature Scale of 1990 was adopted by the International Committee of Weights and Measures at its meeting in 1989, in accordance with the request embodied in Resolution 7 of the 18th General Conference of Weights and Measures of 1987. This scale supersedes the International Practical Temperature Scale of 1968 (amended edition of 1975) and the 1976 Provisional 0.5 K to 30 K Temperature Scale.

1. Units of Temperature

The unit of the fundamental physical quantity known as thermodynamic temperature, symbol T, is the kelvin symbol K, defined as the fraction 1/273.16 of the thermodynamic temperature of the triple point of water1.

Because of the way earlier temperature scales were defined, it remains common practice to express a temperature in terms of its difference from 273.15 K, the ice point. A thermodynamic temperature, T, expressed in this way is known as a Celsius temperature, symbol t, defined by:

t / °C = T / K - 273.15 (1)

The unit of Celsius temperature is the degree Celsius, symbol °C, which is by definition equal in magnitude to the kelvin. A difference of temperature may be expressed in kelvins or degrees Celsius.

The International Temperature Scale of 1990 (ITS-90) defines both International Kelvin Temperatures, symbol T90, and International Celsius Temperatures, symbol T90. The relation between T90 and T90 is the same as that between T and t, i.e.:

t₉₀ / °C = T₉₀ / K - 273.15 (2)

The unit of the physical quantity T90 is the kelvin, symbol K, and the unit of the physical quantity T90 is the degree Celsius, symbol °C, as is the case for the thermodynamic temperature T and the Celsius temperature t.

2. Principles of the International Temperature Scale of 1990 (ITS-90)

The ITS-90 extends upwards from 0.65 K to the highest temperature practicably measurable in terms of the Planck radiation law using monochromatic radiation. The ITS-90 comprises a number of ranges and sub-ranges throughout each of which temperatures T90 are defined. Several of these ranges or sub-ranges overlap, and where such overlapping occurs, differing definitions of T90 exist: these differing definitions have equal status. For measurements of the very highest precision there may be detectable numerical differences between measurements made at the same temperature but in accordance with differing definitions. Similarly, even using one definition, at a temperature between defining fixed points two acceptable interpolating instruments (e.g. resistance thermometers) may give detectably differing numerical values of T90. In virtually all cases these differences are of negligible practical importance and are at the minimum level consistent with a scale of no more than reasonable complexity; for further information on this point see "Supplementary information for the ITS-90" (BIPM-1990).

The ITS-90 has been constructed in such a way that, throughout its range, any given temperature the numerical value of T90 is a close approximation to the numerical value of T90 according to best estimates at the time the scale was adopted. By comparison with direct measurements of thermodynamic temperatures, measurements of T90 are more easily made, are more precise and are highly reproducible.

There are significant numerical differences between the values of T90 and the corresponding values of T90 measured on the International Practical Temperature Scale of 1968 (IPTS-68), see Fig. 1 and Table 6. Similarly there were differences between the IPTS-68 and the International Practical Temperature Scale of 1948 (IPTS-48), and between the International Temperature Scale of 1948 (ITS-48) and the International Temperature Scale of 1927 (ITS-27). See the Appendix, and, for more detailed information, "Supplementary Information for the ITS-90."

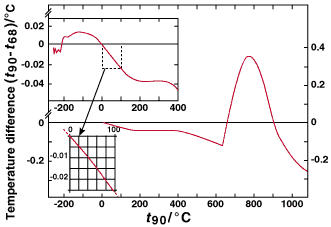
FIG. 1. The differences (t90 - t68) as a function of Celsius temperature t90.

3. Definition of the International Temperature Scale of 1990

Between 0.65 K and 5.0 K T90 is defined in terms of the vapour-pressure temperature relations 3He and 4He.

Between 3.0 K and the triple point of neon (24.5561 K) T90 is defined by means of a helium gas thermometer calibrated at three experimentally realizable temperatures having assigned numerical values (defining fixed points) and using specified interpolation procedures.

Between the triple point of equilibrium hydrogen (13.8033 K) and the freezing point of silver (961.78 °C) T90 is defined by means of platinum resistance thermometers calibrated at specified sets of defining fixed points and using specified interpolation procedures.

Above the freezing point of silver (961.78°C) T90 is defined in terms of a defining fixed point and the Planck radiation law.

The defining fixed points of the ITS-90 are listed in Table 1. The effects of pressure, arising from significant depths of immersion of the sensor or from other causes, on the temperature of most of these points are given in Table 2.

3.1. From 0,65 K: Helium Vapour-Pressure Temperature Equations

In this range T₉₀ is defined in terms of the vapour pressure p of ³He and ⁴He using equations of the form:

9

T90/K = Ao+∑Ai[(in (p/Pa) —B)/C)i

i=1

The values of the constants A₀, A_i, B and C are given in Table 3 for ³He in the range of

0.65 K to 3.2 K, and for ⁴He in the ranges 1.25 K to 2.1768 K (the lambda point) and 2.1768 K to 5.0 K.

3.2 From 3.0 K to the Triple Point of Neon (24.5561 K): Gas Thermometer

In this range T₉₀ is defined in terms of a ³He or a ⁴He gas thermometer of the constant-volume type that has been calibrated at three temperatures. These are the triple point of neon (24.5561 K), the triple point of equilibrium hydrogen (13.8033 K), and a temperature is between 3.0 K and 5.0 K. This last temperature is determined using a 3He or a 4He vapour pressure thermometer as specified in Sect. 3.1.

---

Table 1. Defining fixed points of the ITS-90

	Temperature
Number	T90/K	t90/ºC	Substancea	Stateb	Wr(T90)
1	3 to 5	-270.15 to -268.15	He	V
2	13.8033	-259.3467	e-H2	T	0.001 190 07
3	~17	~-256.15	e-H2 (or He)	V (or G)
4	~20.3	~-252.85	e-H2 (or He)	V (or G)
5	24.5561	-248.5939	Ne	T	0.008 449 74
6	54.3584	-218.7916	O2	T	0.091 718 04
7	83.8058	-189.3442	Ar	T	0.215 859 75
8	234.3156	-38.8344	Hg	T	0.844 142 11
9	273.16	0.01	H2O	T	1.000 000 00
10	302.9146	29.7646	Ga	M	1.118 138 89
11	429.7485	156.5985	In	F	1.609 801 85
12	505.078	231.928	Sn	F	1.892 797 68
13	692.677	419.527	Zn	F	2.568 917 30
14	933.473	660.323	Al	F	3.376 008 60
15	1234.93	961.78	Ag	F	4.286 420 53
16	1337.33	1064.18	Au	F
17	1357.77	1084.62	Cu	F

(a) All substances except ³He are of natural isotopic composition, e-H₂ is hydrogen at the equilibrium concentration of the ortho- and para-molecular forms

(b) For complete definitions and advice on the realization of these various states, see "Supplementary Information for the ITS-90". The symbols have the following meanings: V: vapour pressure point; T: triple point (temperature at which the solid liquid and vapour phases are in equilibrium); G: gas thermometer point; M, F: melting point, freezing point (temperature, at a pressure of 101 325 Pa, at which the solid and liquid phases are in equilibrium)

---

Table 2. Effect of pressure on the temperatures of some defining fixed points⁺

Substance	Assignment value of equilibrium temperature T90/K	Temperature with pressure, p (dT/dp)/ (10-8K · Pa -1)*	Variation with depth, lambda (dT/dl)/ (10-3K · m -1)**
e-Hydrogen (T)	13.8033	34	0.25
Neon (T)	24.5561	16	1.9
Oxygen (T)	54.3584	12	1.5
Argon (T)	83.8058	25	3.3
Mercury (T)	234.3156	5.4	7.1
Water (T)	273.16	- 7.5	- 0.73
Gallium	302.9146	- 2.0	- 1.2
Indium	429.7485	4.9	3.3
Tin	505.078	3.3	2.2
Zinc	692.677	4.3	2.7
Aluminium	933.473	7.0	1.6
Silver	1234.93	6.0	5.4
Gold	1337.33	6.1	10
Copper	1357.77	3.3	2.6

* Equivalent to millikelvins per standard atmosphere

** Equivalent to millikelvins per metre of liquid

+ The Reference pressure for melting and freezing points is the standard atmosphere (p0=101 325 Pa). For triple points (T) the pressure effect is a consequence only of the hydrostatic head of liquid in the cell

---

Table 3. Values of the constants for the helium vapour pressure Eqs. (3), and the temperature range for which each equation, identified by its set of constants, is valid

	3He 0.65 K to 3.2 K	4He 1.25 K to 2.1768 K	4He 2.1768 K to 5.0 K
A0	1.053 447	1.392 408	3.146 631
A1	0.980 106	0.527 153	1.357 655
A2	0.676 380	0.166 756	0.413 923
A3	0.372 692	0.050 988	0.091 159
A4	0.151 656	0.026 514	0.016 349
A5	- 0.002 263	0.001 975	0.001 826
A6	0.006 596	- 0.017 976	- 0.00 4325
A7	0.088 966	0.005 409	- 0.00 4973
A8	- 0.004 770	0.013 259	0
A9	- 0.054 943	0	0
B	7.3	5.6	10.3
C	4.3	2.9	1.9

---

3.2.1. From 4.2 K to the Triple Point of Neon (24.5561 K) with 4He as the Thermometric Gas.

In this range T₉₀ is defined by the relation:

T₉₀ = a + bp +cp², (4)

where p is the pressure in the gas thermometer and a, b and c are coefficients the numerical values of which are obtained from measurements made at the three defining fixed points given in Sect. 3.2. but with the further restriction that the lowest one of these points lies between 4.2 K and 5.0 K.

3.2.2. From 3.0 K to the Triple Point of Neon (24.5561 K) with ³He or ⁴He as the Thermometric Gas.

For a ³He gas thermometer, and for a ⁴He gas thermometer used below 4.2 K, the non-ideality of the gas must be accounted for explicitly, using the appropriate second virial coefficient B3 (T₉₀) or B4 (T₉₀). In this range T₉₀ is defined by the relation:

T₉₀ = a + bp + cp²/1 + B_x(T₉₀) NIV

where p is the pressure in the gas thermometer, a, b and c are coefficients the numerical values of which are obtained from measurements at three defining temperatures as given in Sect. 3.2, N/V is the gas density with N being the quantity of gas and V the volume of the bulb, X is 3 or 4 according to the isotope used, and the values of the second virial coefficients are given by the relations:

For ³He
B(T₉₀)/m³mol^-1={16,69 — 336,98(T₉₀/K)^-1
      +91,04(T₉₀/K)^-2—13,82(T₉₀/K)^-3} 10^-6
For ⁴He
B₄(T₉₀)/m³mol^-1={15,708—374,05(T₉₀/K)^-1
    —383,53(T₉₀/K)^-2-2 + 1799,2(T₉₀/K)^-3
—4033,2(T₉₀/K)^-4 + 3252,8 (T₉₀/K)^-3} 10^-6

---

Table 4. The constants A₀, A_i; B_n, B_i; C₀, C_i; D₀ and D_i in the reference functions of equations (9a); (10a); and (10b) respectively

A0	- 2.135 347 29	B0	0.183 324 722	C0	2.781 572 54	D0	439.932 854
A1	3.183 247 20	B1	0.240 975 303	C1	1.646 509 16	D1	472.418 020
A2	- 1.801 435 97	B2	0.209 108 771	C2	- 0.137 143 90	D2	37.684 494
A3	0.717 272 04	B3	0.190 439 972	C3	- 0.006 497 67	D3	7.472 018
A4	0.503 440 27	B4	0.142 648 498	C4	- 0.002 344 44	D4	2.920 828
A5	- 0.618 993 95	B5	0.077 993 465	C5	0.005 118 68	D5	0.005 184
A6	- 0.053 323 22	B6	0.012 475 611	C6	0.001 879 82	D6	- 0.963 864
A7	0.280 213 62	B7	- 0.032 267 127	C7	- 0.002 044 72	D7	- 0.188 732
A8	0.107 152 24	B8	- 0.075 291 522	C8	- 0.000 461 22	D8	0.191 203
A9	- 0.293 028 65	B9	- 0.056 470 670	C9	0.000 457 24	D9	0.049 025
A10	0.044 598 72	B10	0.076 201 285
A11	0.118 686 32	B11	- 0.123 893 204
A12	- 0.052 481 34	B12	- 0.029 201 193
		B13	- 0.091 173 542
		B14	0.001 317 696
		B15	0.026 025 526

 

The accuracy with which T₉₀ can be realized using Eqs. (4) and (5) depends on the design of the gas thermometer and the gas density used. Design criteria and current good practice required to achieve a selected accuracy are given in "Supplementary Information for the ITS -90".

3.3. The Triple Point of Equilibrium Hydrogen (13.8033 K) to the Freezing Point of Silver (961.78 °C): Platinum Resistance Thermometer

In this range T90 is defined by means of a platinum resistance thermometer calibrated at specified sets of defining fixed points, and using specified reference and deviation functions for interpolation at intervening temperatures.

No single platinum resistance thermometer can provide high accuracy, or is even likely to be usable, over all of the temperature range 13,8033 K to 961.78 °C. The choice of temperature range, or ranges, from among those listed below for which a particular thermometer can be used is normally limited by its construction.

For practical details and current good practice, in particular concerning types of thermometer available, their acceptable operating ranges, probable accuracies, permissible leakage resistance, resistance values, and thermal treatment, see "Supplementary Information for ITS-90". It is particularly important to take account of the appropriate heat treatments that should be followed each time a platinum resistance thermometer is subjected to a temperature above about 420 °C.

Temperatures are determined in terms of the ratio of the resistance R(T₉₀) at a temperature T₉₀ and the resistance R (273.16 K) at the triple point of water.

This ratio, W (T₉₀), is ²:

W(T₉₀)=R(T₉₀)/IR(273,16K)

² Note that this definition of W (T₉₀) differs from the corresponding definition used in the ITS-27, ITS-48, IPTS-48, and IPTS-68: for all of these earlier scales W (T) was defined in terms of reference temperature of 0°C, which since 1954 has itself been defined as 273.15 K

An acceptable platinum resistance thermometer must be made from pure, strain-free platinum, and it must satisfy at least one of the following two relations:

W(27,7646°C)≥1,118,07
W)—38,8344°C)≥0,844 235

An acceptable platinum resistance thermometer that is to be used up to the freezing point of silver must also satisfy the relation:

W(961,78°C)≥4,2844

In each of the resistance thermometer ranges, T₉₀ is obtained from W (T₉₀) as given by the appropriate reference function {Eqs. (9b) or (10b)}, and the deviation W(T₉₀) - Wr(T₉₀). At the defining fixed points this deviation is obtained directly from the calibration of the thermometer: at intermediate temperatures it is obtained by means of the appropriate deviation function {Eqs. (12), (13) and (14)}.

(i) - For the range 13.8033 K to 273.16 K the following reference function is defined:

₁₂         
(9a.)In [W_r(T₉₀)]=A₀ + ∑A_i[In (T₉₀)/273,16K + 1,5/1,5]^i
i=1         

An inverse fnction, equivalent to Eq.(9a.) to within 0,1 mK, is:

₁₅  
(9b.) T₉₀/273,16K = B₀ + ∑ B_i[W_r(T₉₀)^1/6 —0,65/0,35]^i
i=1  

The values of the constants A0, Ai, B0 and Bi are given in Table 4.

A thermometer may be calibrated for use throughout this range or, using progressively fewer calibration points, for ranges with low temperature limits of 24.5561 K, 54.3584 K and 83.8058 K, all having an upper limit of 273.16 K.

(ii) - For the range 0 °C to 961.78 °C the following reference function is defined:

₉  
(10a.) W_r(T₉₀) = C₀ + ∑C_i[T₉₀/K — 754,15/481]^i
i=1  

An inverse function, equivalent to equation (10a.) to within 0,13 mK is:

        ₉
(10b.) T₉₀/K — 273,15 = D₀ + ∑ D_i[W_r(T₉₀) — 2,64/1,64]^{i
        i=1}

The values of the constants C0, Ci, D0 and Di are given in Table 4.

A thermometer may be calibrated for use throughout this range or, using fewer calibration points, for ranges with upper limits of 660.323 °C, 419.527 °C, 231.928 °C, 156.5985 °C or 29.7646 °C, all having a lower limit of 0 °C.

(iii) - A thermometer may be calibrated for use in the range 234.3156 K ( - 38.8344 °C) to 29.7646 °C, the calibration being made at these temperatures and at the triple point of water. Both reference functions {Eqs. (9) and (10)} are required to cover this range.

The defining fixed points and deviation functions for the various ranges are given below, and in summary from in Table 5.

3.3.1. The Triple Point of Equilibrium Hydrogen (13.8033 K) to the Triple Point of Water (273.16 K).

The thermometer is calibrated at the triple points of equilibrium hydrogen (13.8033 K), neon (24.5561 K), oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K), and water (273.16 K), and at two additional temperatures close to 17.0 K and 20.3 K. These last two may be determined either: by using a gas thermometer as described in Sect. 3.2, in which case the two temperatures must lie within the ranges 16.9 K to 17.1 K and 20.2 K to 20.4 K respectively; or by using the vapour pressure-temperature relation of equilibrium hydrogen, in which case the tow temperatures must lie within the ranges 17.025 K to 17.045 K and 20.26 K to 20.28 K respectively, with the precise values being determined from Eqs. (11a) and (11b) respectively:

T₉₀/K - 17.035 = (p/kPa - 33.3213)/13.32 (11a)

T₉₀/K - 20.27 = (p/kPa - 101.292)/30 (11b)

 

(11a.) T₉₀/K — 17,035 = (p/kPa — 33,3213)/13,32
(11b.) T₉₀/K — 20,27 = (p/kPa — 101,292)/30

The deviation function is³
                                                          ₅
(12.) W(T₉₀) — W_r(T₉₀) = a[W(T₉₀)—1] + b[W(T₉₀)—]² + ∑ c_i[In W(T₉₀)]^{i+n
                                                         i=1}

³ This deviation function {and also those of Eqs. (13) and (14)} may be expressed in terms of W_r rather than W; for this procedure see "Supplementary Information for ITS-90"

with values for the coefficients a, b and c_i being obtained from measurements at the defining fixed points and with n = 2.

For this range and for the sub-ranges 3.3.1.1 to 3.3.1.3 the required values W_r(T₉₀) are obtained from Eq. (9a) or from Table 1.

3.3.1.1. The Triple Point of Neon (24.5561 K) to the Triple Point of Water (273.16 K).

The thermometer is calibrated at the triple points of equilibrium hydrogen (13.8033 K), neon (24.5561 K), oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K) and water (273.16 K).

The deviation function is given by Eq. (12) with values for the coefficients a, b, c₁, c₂ and c₃ being obtained from measurements at the defining fixed points and with c₄ = c₅ = n = 0.

3.3.1.2 The Triple Point of Oxygen (54.3584 K) to the Triple Point of Water (273.16 K).

The thermometer is calibrated at the triple points of oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K) and water (273.16 K).

---

Table 5. Deviation functions and calibration points for platinum resistance thermometers in the various ranges in which they define T₉₀

a. Ranges with an upper limit of 273.16 K
Section	Lower temperature limit (T/K)	Deviation functions	Calibration points (see Table 1)
3.3.1	13.8033	As equation (12), with n=2	2-9
3.3.1.1	24.5561	As for 3.3.1 with c4 = c5 = n = 0	2, 5-9
3.3.1.2	54.3584	As for 3.3.1 with c2 = c3 = c4 = c5 = 0, n = 1	6-9
3.3.1.3	83.8058	a[W (T90) - 1]+b[W (T90) - 1] ln W (T90)	7-9
b. Ranges with a lower limit of 0 ºC
Section	Lower temperature limit (t/ºC)	Deviation functions	Calibration points (see Table 1)
3.3.2*	961.78	As equation (14)	9, 12-15
3.3.2.1	660.323	As for 3.3.2 with d = 0	9, 12 - 14
3.3.2.2	419.527	As for 3.3.2 with c = d = 0	9, 12, 13
3.3.2.3	231.928	As for 3.3.2 with c = d = 0	9, 11, 12
3.3.2.4	156.5982	As for 3.3.2 with b = c = d = 0	9, 11
3.3.2.5	29.7646	As for 3.3.2 with b = c = d = 0	9, 10
c. Range from 234.3156 K ( - 38.8344 ºC) to 29.7646 ºC
3.3.3		As for 3.3.2 with c = d = 0	8-10

* Calibration points 9, 12-14 are used with d = 0 for t₉₀ <= 660.323 °C; the values of a, b and c thus obtained are retained for t₉₀ => 660.323 °C with d being determined from calibration point 15

---

The deviation function is given by Eq. (12) with values for the coefficients a, b and c1 being obtained from measurements at the defining fixed points, with c2 = c3 = c4 = c5 = 0 and with n = 1.

3.3.1.3. The Triple Point of Argon (83.8058 K) to the Triple Point of Water (273.16 K).

The thermometer is calibrated at the triple points of argon (83,8058 K), mercury (234,3156 K) and water (273,16 K).

The deviation function is:

(13.) W(T₉₀) — W_r(T₉₀) = a[W(T₉₀)—1] + b[W(T₉₀)—1] In W(T₉₀)

with the values of a and b being obtained from measurements at the defining fixed points.

3.3.2. From 0 °C to the Freezing Point of Silver (961.78 °C).

The thermometer is calibrated at the triple point of water (0,01 °C), and at the freezing points of tin (231.928 °C), zinc (419.527 °C), aluminium (660.323 °C) and silver (961.78 °C).

The deviation function is:

(14.) W(T₉₀) — W_r(T₉₀) = a[W(T₉₀)—1] + b[W(T₉₀)—1]² + c[W(T₉₀)—1]³ + d[W(T₉₀)—W(660,323 °C)]²

For temperatures below the freezing point of aluminium d = 0, with the values of a, b and c being determined from the measured deviations from W_r(T₉₀) at the freezing points of tin, zinc and aluminium. From the freezing point of aluminium to the freezing point of silver the above values of a, b and c are retained and the value of d is determined from the measured deviation from W_r(T₉₀) at the freezing point of silver.

For this range and for the sub-ranges 3.3.2.1 to 3.3.2.5 the required values for W_r(T₉₀) are obtained from Eq. (10a) or from Table 1.

3.3.2.1. From 0 °C to the Freezing Point of Aluminium (660.323 °C).

The thermometer is calibrated at the triple point of water (0.01 °C), and at the freezing points of tin (231.928 °C), zinc (419.527 °C) and aluminium (660.323 °C).

The deviation function is given by Eq. (14), with the values of a, b and c being determined from measurements at the defining fixed points and with d = 0.

3.3.2.2. From 0 °C to the Freezing Point of Zinc (419.527 °C).

The thermometer is calibrated at the triple point of water (0.0 °C), and at the freezing points of tin (231.928 °C). and zinc (419.527 °C).

The deviation function is given by Eq. (14), with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.

3.3.2.3. From 0 °C to the Freezing Point of Tin (231.928 °C).

The thermometer is calibrated at the triple point of water (0.01 °C), and at the freezing points of indium (156.5985 °C) and tin (231.928 °C).

The deviation function is given by Eq. (14), with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.

3.3.2.4.From 0 °C to the Freezing Point of Indium (156,5985 °C).

The thermometer is calibrated at the triple point of water (0.01 °C), and at the freezing point of indium (156.5985 °C).

The deviation function is given by Eq. (14) with the value of a being obtained from measurements at the defining fixed points and with b = c = d = 0.

3.3.2.5. From 0 °C to the Melting Point of Gallium (29.7646 °C).

The thermometer is calibrated at the triple point of water (0.01 °C), and the melting point of gallium (29.7646 °C).

The deviation function is given by Eq. (14) with the value of a being obtained from measurements at the defining fixed points and with b = c = d = 0.

3.3.3. The Triple Point of Mercury (-38.8344 °C) to the Melting Point of Gallium (29.7646 °C).

The thermometer is calibrated at the triple points of mercury (- 38.8344 °C), and water (0.01 °C), and at the melting point of gallium (29.7646 °C).

The deviation function is given by Eq. (14) with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.

The required values of W_r(T₉₀) are obtained from Eqs. (9a) and (10a) for measurements below and above 273.16 K respectively, or from Table 1.

3.4. The Range Above the Freezing Point of Silver (961,78 °C): Planck Radiation Law

Above the freezing point of silver the temperature T90 is defined by the equation:

(15.) Lλ(T₉₀)/Lλ[(T₉₀(X)]=exp(c₂[λT₉₀(X)]^-1)—1/exp(c₂[λT₉₀]^-1)—1

where T₉₀(X) refers to any one of the silver {T90(Ag) = 1234.93 K}, the gold {T₉₀(Au) = 1337.33 K} or the copper {T90(Cu) = 1357.77 K} freezing points4 and in which Llambda(T₉₀) and Llambda[T₉₀(X)] are the spectral concentrations of the radiance of a blackbody at the wavelength (in vacuo) lambda at T₉₀ and at T₉₀(X) respectively, and c₂ = 0.014388 m • K

. For practical details and current good practice for optical pyrometry, see "Supplementary Information for the ITS-90" (BIPM-1990).

4 The T₉₀ values of the freezing points of silver, gold and copper are believed to be self consistent to such a degree that the substitution of any one of them in place of one of the other two as the reference temperature T₉₀(X) will not result in significant differences in the measured values of T₉₀.

4. Supplementary Information and Differences from Earlier Scales

The apparatus, methods and procedures that will serve to realize the ITS-90 are given in "Supplementary Information for the ITS-90". This document also gives an account of the earlier International Temperature Scales and the numerical differences between successive scales that include, where practicable, mathematical functions for differences T₉₀ - T68. A number of useful approximations to the ITS-90 are given in "Techniques for Approximating the ITS-90".

These two documents have been prepared by the Comité Consultatif de Thermométrie and are published by the BIPM; they are revised and updated periodically. The differences T₉₀ - T₆₈ are shown in Fig. 1 and Table 6. The number of significant figures given in Table 6 allows smooth interpolations to be made. However, the reproducibility of the IPTS-68 is, in many areas, substantially worse than is implied by this number.

---

Table 6. Differences between ITS-90 and EPT-76, and between ITS-90 and IPTS-68 for specified values of T₉₀ and t₉₀.

(T90 - T76)/mK
T90/K	0	1	2	3	4	5	6	7	8	9
0						-0.1	-0.2	-0.3	-0.4	-0.5
10	-0.6	-0.7	-0.8	-1.0	-1.1	-1.3	-1.4	-1.6	-1.8	-2.0
20	-2.2	-2.5	-2.7	-3.0	-3.2	-3.5	-3.8	-4.1
(T90 - T68)/K
T90/K	0	1	2	3	4	5	6	7	8	9
10					-0.006	-0.003	-0.004	-0.006	-0.008	-0.009
20	-0.009	-0.008	-0.007	-0.007	-0.006	-0.005	-0.004	-0.004	-0.005	-0.006
30	-0.006	-0.007	-0.008	-0.008	-0.008	-0.007	-0.007	-0.007	-0.006	-0.006
40	-0.006	-0.006	-0.006	-0.006	-0.006	-0.007	-0.007	-0.007	-0.006	-0.006
50	-0.006	-0.005	-0.004	-0.004	-0.003	-0.002	-0.001	0.000	0.001	0.002
60	0.003	0.003	0.004	0.004	0.005	0.005	0.006	0.006	0.007	0.007
70	0.007	0.007	0.007	0.007	0.007	0.008	0.008	0.008	0.008	0.008
80	0.008	0.008	0.008	0.008	0.008	0.008	0.008	0.008	0.008	0.008
90	0.008	0.008	0.008	0.008	0.008	0.008	0.008	0.009	0.009	0.009
T90/K	0	10	20	30	40	50	60	70	80	90
100	0.009	0.011	0.013	0.014	0.014	0.014	0.014	0.013	0.012	0.012
200	0.011	0.010	0.009	0.008	0.007	0.005	0.003	0.001
(t90 - t68)/ºC
t90/ºC	0	-10	-20	-30	-40	-50	-60	-70	-80	-90
-100	0.013	0.013	0.014	0.014	0.014	0.013	0.012	0.010	0.008	0.008
0	0.000	0.002	0.004	0.006	0.008	0.009	0.010	0.011	0.012	0.012
t90/ºC	0	10	20	30	40	50	60	70	80	90
0	0.000	-0.002	-0.005	-0.007	-0.010	-0.013	-0.016	-0.018	-0.021	-0.024
100	-0.026	-0.028	-0.030	-0.032	-0.034	-0.036	-0.037	-0.038	-0.039	-0.039
200	-0.040	-0.040	-0.040	-0.040	-0.040	-0.040	-0.040	-0.039	-0.039	-0.039
300	-0.039	-0.039	-0.039	-0.040	-0.040	-0.041	-0.042	-0.043	-0.045	-0.046
400	-0.048	-0.051	-0.053	-0.056	-0.059	-0.062	-0.065	-0.068	-0.072	-0.075
500	-0.079	-0.083	-0.087	-0.090	-0.094	-0.098	-0.101	-0.105	-0.108	-0.112
600	-0.115	-0.118	-0.122	- 0.125*	-0.08	-0.03	0.02	0.06	0.11	0.16
700	0.20	0.24	0.28	0.31	0.33	0.35	0.36	0.36	0.36	0.35
800	0.34	0.32	0.29	0.25	0.22	0.18	0.14	0.10	0.06	0.03
900	-0.01	-0.03	-0.06	-0.08	-0.10	-0.12	-0.14	-0.16	-0.17	-0.18
1000	-0.19	-0.20	-0.21	-0.22	-0.23	-0.24	-0.25	-0.25	-0.26	-0.26
t90/ºC	0	100	200	300	400	500	600	700	800	900
1000		-0.26	-0.30	-0.35	-0.39	-0.44	-0.49	-0.54	-0.60	-0.66
2000	-0.72	-0.79	-0.85	-0.93	-1.00	-1.07	-1.15	-1.24	-1.32	-1.41
3000	-1.50	-1.59	-1.69	-1.78	-1.89	-1.99	-2.10	-2.21	-2.32	-2.43

* A discontinuity in the first derivative of (t₉₀ - t₆₈) occurs at a temperature of t90 = 630.6 °C, at which (t₉₀ - t₆₈) = - 0.125 °C

---

Appendix

The International Temperature Scale of 1927 (ITS-27)

The International Temperature Scale of 1927 was adopted by the seventh General Conference of Weights and Measures to overcome the practical difficulties of the direct realization of thermodynamic temperatures by gas thermometry, and as a universally acceptable replacement for the differing existing national temperature scales. The ITS-27 was formulated so as to allow measurements of temperature to be made precisely and reproducibly, with as close an approximation to thermodynamic temperatures as could be determined at that time. Between the oxygen boiling point and the gold freezing point it was based upon a number of reproducible temperatures, or fixed points, to which numerical values were assigned, and two standard interpolating instruments. Each of these interpolating instruments was calibrated at several of the fixed points, this giving the constants for the interpolating formula in the appropriate temperature range. A platinum resistance thermometer was used for the low part and a platinum rhodium/platinum thermocouple for temperatures above 660 °C. For the region above the gold freezing point, temperatures were defined in terms of the Wien radiation law: in practice, this invariably resulted in the selection of an optical pyrometer as the realizing instrument.

The International Temperature Scale of 1948 (ITS-48)

The International Temperature Scale of 1948 was adopted by the ninth General Conference. Changes from the ITS-27 were: the lower limit of platinum resistance thermometer range was changed from -190 °C to the defined oxygen boiling point of -182.97 °C, and the junction of the platinum resistance thermometer range and the thermocouple range became the measured antimony freezing point (about 630 °C) in place 660 °C; the silver freezing point was defined as being 960.8 °C instead of 960.5 °C; the gold freezing point replaced the gold melting point (1063 °C); the Planck radiation law replaced the Wien law; the value assigned to the second radiation constant became 1.438 x 10-2 m • K in place of 1,432 x 10-2 m • K the permitted ranges for the constants of the interpolation formula for the standard resistance thermometer and thermocouple were modified; the limitation on lT for optical pyrometry (lambda•T<3x10-3 m • K) was changed on the requirement that "visible" radiation be used.

The International Practical Temperature Scale of 1948 (Amended Edition of 1960) (IPTS-48)

The International Practical Temperature Scale of 1948, amended edition of 1960, was adopted by the eleventh General Conference: the tenth General Conference had already adopted the triple point of water as the sole point defining the kelvin, the unit of thermodynamic temperature. In addition to the introduction of the word "Practical", the modifications to the ITS-48 were: the triple point of water, defined as being 0.01 °C, replaced the freezing point of zinc, defined as being 419.505 °C, became a preferred alternative to the sulphur boiling point (444.6 °C) as a calibration point; the permitted ranges for the constants of the interpolation formulae for the standard resistance thermometer and the thermocouple were further modified; the restriction to "visible" radiation for optical pyrometry was removed.

Inasmuch as the numerical values of temperature on the IPTS-48 were the same as on the ITS-48, the former was not a revision of the scale of 1948 but merely an amended form of it.

The International Practical Temperature Scale of 1968 (IPTS-68)

In 1968 the International Committee of Weights and Measures promulgated the International Practical Temperature Scale of 1968, having been empowered to do so by the thirteenth General Conference of 1967 - 1968. The IPTS-68 incorporated very extensive changes from the IPTS-48. These included numerical changes, designed to bring to more nearly in accord with thermodynamic temperatures, that were sufficiently large to be apparent to many users. Other changes were as follows: the lower limit of the scale was extended down to 13.81 K; at even lower temperatures (0.5 K to 5.2 K), the use of two helium vapour pressure scales was recommended; six new defining fixed points were introduced - the triple point of equilibrium hydrogen (13.81 K), an intermediate equilibrium hydrogen point (17.042 K), the normal boiling point of equilibrium hydrogen (20.28 K), the boiling point of neon (27.102 K), the triple point of oxygen (54.361 K), and the freezing point of tin (231.9681 °C) which became a permitted alternative to the boiling point of water; the boiling point of sulphur was deleted; the values assigned to four fixed points were changed - the boiling point of oxygen (90.188 K), the freezing point of zinc (419.58 °C), the freezing point of silver (961.93 °C), and the freezing point of gold (1064.43 °C): the interpolating formulae for the resistance thermometer range became much more complex; the value assigned to the second radiation constant c2 became 1.4388 x 10-2 m • K; the permitted ranges of the constants for the interpolation formulae for the resistance thermometer and thermocouple were again modified.

The International Practical Temperature Scale of 1968 (Amended Edition of 1975) (IPTS-68)

The International Practical Temperature Scale of 1968, amended edition of 1975, was adopted by the fifteenth General Conference in 1975. As was the case for the IPTS-48 with respect to the ITS-48, the IPTS-68 (75) introduced no numerical changes. Most of the extensive textural changes were; the oxygen point was defined as the condensation point rather than the boiling point; the triple point of argon (83.798 K) was introduced as a permitted alternative to the condensation point of oxygen; new values of the isotopic composition of naturally occurring neon were adopted; the recommendation to use values of T given by the 1958 4He and 1962 3He vapour-pressure scales was rescinded.

The 1976 Provisional 0.5 K to 30 K Temperature Scale (EPT-76)

The 1976 Provisional 0.5 K to 30 K Temperature Scale was introduced to meet two important requirements: these were to provide means of substantially reducing the errors (with respect to corresponding thermodynamic values) below 27 K that were then known to exist in the IPTS-68 and throughout the temperature ranges of the 4He and 3He vapour pressure scales of 1958 and 1962 respectively, and to bridge the gap between 5.2 K and 13.81 K in which there had not previously been an international scale. Other objectives in devising the ETP-76 were "that it should be thermodynamically smooth, that it should be continuous with the IPTS-68 at 27.1 K, and that is should agree with thermodynamic temperature T as closely as these two conditions allow". In contrast with the IPTS-68, and to ensure its rapid adoption, several methods of realizing the ETP-76 were approved. These included: using a thermodynamic interpolation instrument and one or more of eleven assigned reference points; taking differences from the IPTS-68 above 13.81 K; taking differences from certain well-established laboratory scales. Because there was a certain "lack of internal consistency" it was admitted that "slight ambiguities between realizations" might be introduced. However the advantages gained by adopting the EPT-76 as a working scale until such time as the IPTS-68 should be revised and extended were considered to outweigh the disadvantages.