Technology Overview

In an effort to improve performance, some instrumentation manufacturers are exploring the value of using “fuzzy logic” for process control. This OMEGA Engineering White Paper explores both the weaknesses of PID systems and the potential benefits of fuzzy logic controllers, with particular reference to issues in temperature control. Individual sections address:
- PID challenges
- Introduction to fuzzy logic for control
- PID plus adaptive fuzzy logic
- Applications
PID Challenges
The mathematics in a PID control equation is complex with multiple variables and constants interacting. In any given application these are selected to follow the target value as closely as possible, within the constraints imposed by the process itself and the instrumentation.
Three issues common to almost every process control application are:
Three issues common to almost every process control application are:
- Time delays or lag
- Step function response
- “Ramp & Soak” function response

When the target value changes instantaneously PID forces the system to apply a large correcting factor, which again can lead to overshoot. Alternatively, the system may become saturated, unable to supply sufficient correction, adding to the impact of the “I” term.
These problems also occur in “ramp & soak” situations where temperature is increased gradually then held. Tracking a gradual change in setpoint can challenge PID control systems.
As a result, selecting the optimal values is something of a trial-and-error process known as “tuning.” Over the years many approaches to tuning have been developed, the most satisfactory of which appears to be the “Ziegler Nichols” method. However, this produces high levels of oscillation, which can be problematic in some situations.
Introduction to Fuzzy Logic Control
Fuzzy Logic is a particular
area of concentration in the study of Artificial Intelligence
and is based on the value of that information which is neither
definitely true nor false. The information which humans use in
their everyday lives to base intuitive decisions and apply general
rules of thumb can and should be applied to those control situations
which demand them. Acquired knowledge can be a powerful weapon
to combat the undesired effects of the system response.
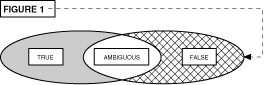 Fuzzy logic controllers use a very flexible set of if-then
rules. The solution is then applied to appropriate membership
functions. Referring to figure 1, values which lie within the
shaded area are called true beyond a shadow of a doubt.
Fuzzy logic controllers use a very flexible set of if-then
rules. The solution is then applied to appropriate membership
functions. Referring to figure 1, values which lie within the
shaded area are called true beyond a shadow of a doubt.
Those values which lie within the cross hatched area are called false beyond a shadow of a doubt. If all data falls to one side or the other of the overlap area, then Fuzzy Logic probably would be of little benefit.
In most applications there are some points which lie in the common area. Information which lies within the common area has to be studied, stored, and used to quantify and to classify the data. This allows for smart manipulation of the data structure in order to make inference to a solution. Information which falls in that common area can be ranked, aged, and "best guess" made after evaluation of this "gray" information.
 Another
advantage of Fuzzy Logic controllers is to quantify the
input signal in a sometimes "noisy" environment. This noise, which
tends to corrupt the integrity of the actual signal, is dealt
with through the common sense of the competent operator. Mathematically,
the information must be judged and prepared for use in decision
making. If an operator took the time to plot the process information
on an X-Y coordinate system, the operator could visually apply
a curve fit to the data and come up with a fairly accurate generic
representation.
Another
advantage of Fuzzy Logic controllers is to quantify the
input signal in a sometimes "noisy" environment. This noise, which
tends to corrupt the integrity of the actual signal, is dealt
with through the common sense of the competent operator. Mathematically,
the information must be judged and prepared for use in decision
making. If an operator took the time to plot the process information
on an X-Y coordinate system, the operator could visually apply
a curve fit to the data and come up with a fairly accurate generic
representation.
Mathematically, fitting a curve of lower order would produce a fairly inaccurate representation. Therefore, a higher order curve fit would be appropriate to accommodate the noisy signal. Fuzzy Logic attempts to emulate what the human response would be and apply the most intelligent fit to the data.
Conventional computing is based on Boolean logic, meaning everything is represented as either zero or one. In some situations this leads to oversimplification and inadequate results. Fuzzy logic controllers, and by extension, fuzzy control, seeks to deal with complexity by creating heuristics that align more closely with human perception of problems.
Fuzzy logic provides a way of dealing with imprecision and nonlinearity in complex control situations. Inputs are passed to an “inference engine” where human or experienced-based rules are applied to produce an output.
 Fuzzy logic controllers use a very flexible set of if-then
rules. The solution is then applied to appropriate membership
functions. Referring to figure 1, values which lie within the
shaded area are called true beyond a shadow of a doubt.
Fuzzy logic controllers use a very flexible set of if-then
rules. The solution is then applied to appropriate membership
functions. Referring to figure 1, values which lie within the
shaded area are called true beyond a shadow of a doubt. Those values which lie within the cross hatched area are called false beyond a shadow of a doubt. If all data falls to one side or the other of the overlap area, then Fuzzy Logic probably would be of little benefit.
In most applications there are some points which lie in the common area. Information which lies within the common area has to be studied, stored, and used to quantify and to classify the data. This allows for smart manipulation of the data structure in order to make inference to a solution. Information which falls in that common area can be ranked, aged, and "best guess" made after evaluation of this "gray" information.
 Another
advantage of Fuzzy Logic controllers is to quantify the
input signal in a sometimes "noisy" environment. This noise, which
tends to corrupt the integrity of the actual signal, is dealt
with through the common sense of the competent operator. Mathematically,
the information must be judged and prepared for use in decision
making. If an operator took the time to plot the process information
on an X-Y coordinate system, the operator could visually apply
a curve fit to the data and come up with a fairly accurate generic
representation.
Another
advantage of Fuzzy Logic controllers is to quantify the
input signal in a sometimes "noisy" environment. This noise, which
tends to corrupt the integrity of the actual signal, is dealt
with through the common sense of the competent operator. Mathematically,
the information must be judged and prepared for use in decision
making. If an operator took the time to plot the process information
on an X-Y coordinate system, the operator could visually apply
a curve fit to the data and come up with a fairly accurate generic
representation. Mathematically, fitting a curve of lower order would produce a fairly inaccurate representation. Therefore, a higher order curve fit would be appropriate to accommodate the noisy signal. Fuzzy Logic attempts to emulate what the human response would be and apply the most intelligent fit to the data.
Conventional computing is based on Boolean logic, meaning everything is represented as either zero or one. In some situations this leads to oversimplification and inadequate results. Fuzzy logic controllers, and by extension, fuzzy control, seeks to deal with complexity by creating heuristics that align more closely with human perception of problems.
Fuzzy logic provides a way of dealing with imprecision and nonlinearity in complex control situations. Inputs are passed to an “inference engine” where human or experienced-based rules are applied to produce an output.
PID Plus Adaptive Fuzzy Logic
Tuning of PID loops depends on heuristics yet often ends up being sub-optimal. Fuzzy logic provides an alternative to approaches such as Ziegler Nichols, and a growing body of research suggests it yields superior results. Thus it would seem an ideal way to control many complex processes is with a PID controller tuned with fuzzy logic.
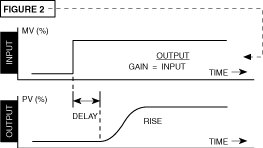
 Ziegler-Nichols
control theory provides for PID (proportional, integral, and derivative)
numbers which aid in the operation of controls. The development
of the inexpensive microprocessor based PID control has replaced
a majority of the thermostat (on/off) type devices. Most controllers
that are microprocessor based have an autotune function which
operates a system experiment as shown in figure 2.
Ziegler-Nichols
control theory provides for PID (proportional, integral, and derivative)
numbers which aid in the operation of controls. The development
of the inexpensive microprocessor based PID control has replaced
a majority of the thermostat (on/off) type devices. Most controllers
that are microprocessor based have an autotune function which
operates a system experiment as shown in figure 2.
This experiment helps to determine the thermal characteristics of a particular system. In most cases, the method of autotune is to make a step input into the final control element and monitor the output. This produces a gain term directly related to proportional band. A delay time between the application of the step input and an observed response influences the derivative number. The rise time of the response to the step input produces a value to be used in integration.
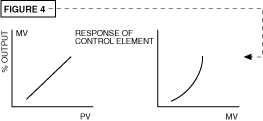
In some systems, the delay time to produce response is much different than the time to give up heat as shown in figure 3. This is common with many extruder applications making a Fuzzy Logic approach quite beneficial. If the response of the final control element as shown in figure 4 is nonlinear, for whatever reason, a linear response from proportioning action only would result in less than acceptable control.
In addition, if the system tends to have changing thermal properties or some thermal irregularities, a Fuzzy Logic controller should offer a better alternative to the constant adjustment of PID parameters. Most Fuzzy Logic software begins building its information base during the autotune function. In fact, the majority of the information used in the early stages of system startup come from the autotune solutions.
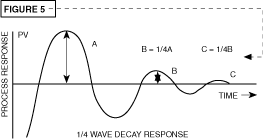 Until
Looking at the typical response
of a standard PID control strategy, shown in figure 5, the response
curve demonstrates a quarter wave decay phenomenon. This method
works adequately in the steady state. However, in real applications
the overshoot and undershoot may sometimes be unacceptable.
Until
Looking at the typical response
of a standard PID control strategy, shown in figure 5, the response
curve demonstrates a quarter wave decay phenomenon. This method
works adequately in the steady state. However, in real applications
the overshoot and undershoot may sometimes be unacceptable.
Methods derived prior to Fuzzy Logic involve setpoint adjustment to control this oscillation below a critical level. Ramp to setpoint was introduced into single loop controls to reduce the rate of ascent of the process variable in order to knock down the initial overshoot. Finally, slight detuning of the steady state PID parameters is commonly done to minimize the destructive oscillatory response. Fuzzy Logic controllers can incorporate an intelligent response to deal with these situations.
A single feedback control architecture, some of the obvious information which is readily available to the algorithms is; the error signal, the difference between Fuzzy Logic, the process variable and the setpoint variable; change in error from previous cycles to the current cycle; changes to the setpoint variable; change of the manipulated variable from cycle to cycle; as well as the change in the process from past to present.
Also available, in addition to the above, are the multiple combinations of the system response data. As long as the irregularity lies in that dimension which fuzzy decisions are being based or associated, the result should be enhanced performance. This enhanced performance should be demonstrated in both the transient and steady state response.
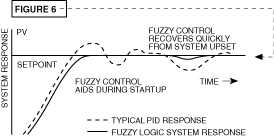 With
The
benefit of accumulating system information is the capability to
predict a problem or upset developing rather than waiting until
the unwanted situation is fully underway as seen in figure 6.
A simple analogy to this type of action is to consult your medical
expert immediately if you experience any symptoms of heart trouble
such as shortness of breath, dizziness, or chest pain rather than
waiting until you are experiencing myocardial infarction.
With
The
benefit of accumulating system information is the capability to
predict a problem or upset developing rather than waiting until
the unwanted situation is fully underway as seen in figure 6.
A simple analogy to this type of action is to consult your medical
expert immediately if you experience any symptoms of heart trouble
such as shortness of breath, dizziness, or chest pain rather than
waiting until you are experiencing myocardial infarction.
Early preventative care just makes good sense. The same holds true for control theory. Fuzzy Logic should offer more intelligent control now, when it is needed, rather than waiting until the problem has become catastrophic.
One commercially available product incorporating such an approach is the OMEGA® Platinum Series of temperature and process controllers. This family of compact microprocessorbased PID-fuzzy logic controllers, available in three DIN sizes, is designed to be easy to set-up and use. All common thermocouples and RTDs can be connected, with the system automatically enabling only the relevant functions for the input type selected. Voltage and current inputs are also available, allowing use with almost any engineering units. These controllers provide a complete PID solution, supporting complex programs with up to 16 Ramp & Soak sequences. Auto tune is available for PID applications with adaptive fuzzy logic to help attain optimal results.
 Ziegler-Nichols
control theory provides for PID (proportional, integral, and derivative)
numbers which aid in the operation of controls. The development
of the inexpensive microprocessor based PID control has replaced
a majority of the thermostat (on/off) type devices. Most controllers
that are microprocessor based have an autotune function which
operates a system experiment as shown in figure 2.
Ziegler-Nichols
control theory provides for PID (proportional, integral, and derivative)
numbers which aid in the operation of controls. The development
of the inexpensive microprocessor based PID control has replaced
a majority of the thermostat (on/off) type devices. Most controllers
that are microprocessor based have an autotune function which
operates a system experiment as shown in figure 2. This experiment helps to determine the thermal characteristics of a particular system. In most cases, the method of autotune is to make a step input into the final control element and monitor the output. This produces a gain term directly related to proportional band. A delay time between the application of the step input and an observed response influences the derivative number. The rise time of the response to the step input produces a value to be used in integration.
In some systems, the delay time to produce response is much different than the time to give up heat as shown in figure 3. This is common with many extruder applications making a Fuzzy Logic approach quite beneficial. If the response of the final control element as shown in figure 4 is nonlinear, for whatever reason, a linear response from proportioning action only would result in less than acceptable control.
In addition, if the system tends to have changing thermal properties or some thermal irregularities, a Fuzzy Logic controller should offer a better alternative to the constant adjustment of PID parameters. Most Fuzzy Logic software begins building its information base during the autotune function. In fact, the majority of the information used in the early stages of system startup come from the autotune solutions.
 Until
Looking at the typical response
of a standard PID control strategy, shown in figure 5, the response
curve demonstrates a quarter wave decay phenomenon. This method
works adequately in the steady state. However, in real applications
the overshoot and undershoot may sometimes be unacceptable.
Until
Looking at the typical response
of a standard PID control strategy, shown in figure 5, the response
curve demonstrates a quarter wave decay phenomenon. This method
works adequately in the steady state. However, in real applications
the overshoot and undershoot may sometimes be unacceptable. Methods derived prior to Fuzzy Logic involve setpoint adjustment to control this oscillation below a critical level. Ramp to setpoint was introduced into single loop controls to reduce the rate of ascent of the process variable in order to knock down the initial overshoot. Finally, slight detuning of the steady state PID parameters is commonly done to minimize the destructive oscillatory response. Fuzzy Logic controllers can incorporate an intelligent response to deal with these situations.
A single feedback control architecture, some of the obvious information which is readily available to the algorithms is; the error signal, the difference between Fuzzy Logic, the process variable and the setpoint variable; change in error from previous cycles to the current cycle; changes to the setpoint variable; change of the manipulated variable from cycle to cycle; as well as the change in the process from past to present.
Also available, in addition to the above, are the multiple combinations of the system response data. As long as the irregularity lies in that dimension which fuzzy decisions are being based or associated, the result should be enhanced performance. This enhanced performance should be demonstrated in both the transient and steady state response.
 With
The
benefit of accumulating system information is the capability to
predict a problem or upset developing rather than waiting until
the unwanted situation is fully underway as seen in figure 6.
A simple analogy to this type of action is to consult your medical
expert immediately if you experience any symptoms of heart trouble
such as shortness of breath, dizziness, or chest pain rather than
waiting until you are experiencing myocardial infarction.
With
The
benefit of accumulating system information is the capability to
predict a problem or upset developing rather than waiting until
the unwanted situation is fully underway as seen in figure 6.
A simple analogy to this type of action is to consult your medical
expert immediately if you experience any symptoms of heart trouble
such as shortness of breath, dizziness, or chest pain rather than
waiting until you are experiencing myocardial infarction. Early preventative care just makes good sense. The same holds true for control theory. Fuzzy Logic should offer more intelligent control now, when it is needed, rather than waiting until the problem has become catastrophic.
One commercially available product incorporating such an approach is the OMEGA® Platinum Series of temperature and process controllers. This family of compact microprocessorbased PID-fuzzy logic controllers, available in three DIN sizes, is designed to be easy to set-up and use. All common thermocouples and RTDs can be connected, with the system automatically enabling only the relevant functions for the input type selected. Voltage and current inputs are also available, allowing use with almost any engineering units. These controllers provide a complete PID solution, supporting complex programs with up to 16 Ramp & Soak sequences. Auto tune is available for PID applications with adaptive fuzzy logic to help attain optimal results.
Applications

The advantage of this approach takes the need for the operator to understand the theory of fuzzy operation away. Operation only requires the application of common knowledge to the standard parameters. A few products which have benefited from the implementation of Fuzzy Logic are: camcorders with automatic compensation for operator injected noise such as shaking and moving; elevators with decreased wait time, making intelligent floor decisions and minimizing travel and power consumption; anti lock braking systems with quick reacting independent wheel decisions based on current and acquired knowledge; television with automatic color, brightness, and acoustic control based on signal and environmental conditions; and finally, most importantly to this article, single loop temperature and process controls.
Unless open-loop control is acceptable, almost every process control application would benefit from PID control. In terms of temperature control, good examples are:

- Heat treatment of metals. “Ramp & Soak” sequences need precise control to ensure desired metallurgical properties are achieved.
- Drying/evaporating solvents from painted surfaces. Over-temperature conditions can damage substrates while low temperatures can result in product damage and poor appearance.
- Curing rubber. Precise temperature control ensures complete cure is achieved without adversely affecting material properties.
- Baking. Commercial ovens must follow tightly prescribed heating and cooling sequences to ensure the necessary reactions take place.
- Ceramics. Continuous kilns must deliver high levels of heat yet are subject to varying thermal loads. This makes them an ideal application for PID control.
In addition, many scientific and chemical processes rely on careful and accurate temperature control using fuzzy logic.
Key Takeaways

PID control is an established method of providing such control, but requires tuning for optimal performance. Such tuning is complex and difficult so heuristic techniques, such as the Ziegler Nichols method, are usually employed.
Processes requiring step change or “Ramp & Soak” control are especially difficult to handle through conventional PID techniques. To address this, controller manufacturers like OMEGA are incorporating auto tuning capabilities to fuzzy logic controllers. Advanced computational techniques are used to help optimize PID loops, and provide improved levels of process control.
 CLOSE
CLOSE










 Omega's relationship with Rutgers sprouted with their goals in substituting manual processes with an IoT solution for hands-off data collection capabilities.
Omega's relationship with Rutgers sprouted with their goals in substituting manual processes with an IoT solution for hands-off data collection capabilities.
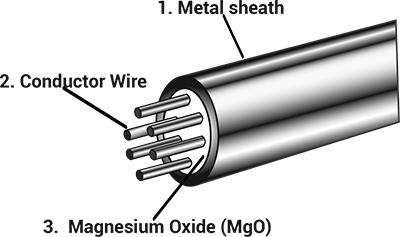 MI cables are used in high temperature or high pressure harsh environments for a good reason, here's why:
MI cables are used in high temperature or high pressure harsh environments for a good reason, here's why: